A Varies Inversely As R

Hotmath

• Habitation

Inverse Variation

While straight variation describes a linear relationship between two variables , inverse variation describes some other kind of relationship.

For ii quantities with inverse variation, as one quantity increases, the other quantity decreases.

For case, when you lot travel to a detail location, as your speed increases, the fourth dimension it takes to get in at that location decreases. When you decrease your speed, the time it takes to arrive at that location increases. So, the quantities are inversely proportional.

An inverse variation can be represented by the equation $xy=k$ or $y=\frac{\mathrm{thou}}{x}$ .

That is, $y$ varies inversely as $\mathrm{ten}$ if in that location is some nonzero constant $k$ such that, $\mathrm{10}y=\mathrm{1000}$ or $y=\frac{g}{x}$ where $\mathrm{ten}\ne 0,y\ne 0$ .

Suppose $y$ varies inversely equally $x$ such that $\mathrm{10}y=3$ or $y=\frac{\mathrm{iii}}{\mathrm{10}}$ . That graph of this equation shown.

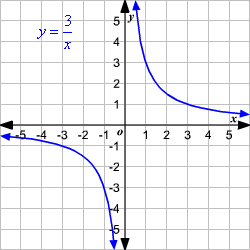
Since $\mathrm{chiliad}$ is a positive value, every bit the values of $x$ increase, the values of $y$ subtract.

Annotation: For direct variation equations, y'all say that $y$ varies directly as $x$ . For inverse variation equations, you say that $y$ varies inversely as $\mathrm{10}$ .

Production Rule for Inverse Variation

If $\left(x_1,y_{\mathrm{i}}\right)$ and $\left(x_2,y_2\right)$ are solutions of an inverse variation, then $x_{\mathrm{one}}{y}_1=\mathrm{1000}$ and $x_{\mathrm{ii}}{y}_2=k$ .

Substitute ${\mathrm{10}}_{\mathrm{one}}{y}_1$ for $k$ .

$x_1{y}_1=x_2{y}_{\mathrm{two}}$ or $\frac{x_1}{{\mathrm{10}}_{\mathrm{two}}}=\frac{y_{\mathrm{two}}}{y_{\mathrm{i}}}$

The equation $x_{\mathrm{i}}{y}_1={\mathrm{10}}_2{y}_2$ is chosen the product rule for inverse variations.

Instance:

In a manufactory, $10$ men can do the job in $30$ days. How many days it will have if $20$ men do the same job?

Hither, when the human being ability increases, they will need less than $30$ days to complete the aforementioned job. And then, this is an changed variation.

Let $x$ be the number of men workers and let $y$ exist the number of days to consummate the piece of work.

And then, $x_1=10,{\mathrm{ten}}_2=20$ and $y_{\mathrm{ane}}=30$ .

By the product rule of changed variation,

$\begin{array}{l}\left(10\right)\left(\mathrm{xxx}\right)=\left(\mathrm{xx}\right)\left(y_2\right)\\ 300=20y_2\end{array}$

Solve for $y_2$ .

$\begin{array}{l}{y}_2=\frac{300}{20}\\ =\mathrm{fifteen}\end{array}$

Therefore, $20$ men can practice the same job in $15$ days.

A Varies Inversely As R,

Source: https://www.varsitytutors.com/hotmath/hotmath_help/topics/inverse-variation

Posted by: carterhinatimsee.blogspot.com

Share this post